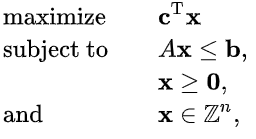Extracting meaning from text of recipe ingredients

Concerning Descriptive Analytics, using Python on 2018/10/01

text algorithms

A unsupervised approach to extracting core tokens from text (specifically the base of an ingredient description).

• Background
• Overview
• Setup
  • Data acquisition
  • Data cleaning
• First Approach (miserable failure)
  • Formulation
  • Inputs
  • Creating the IP
  • Results
• Second Approach (moderate success)
  • Inputs
  • Process
  • Results
• Conclusions
• Code

Background

A few months ago, I wrote my first post using R, which performed a basic analysis on data scraped from Allrecipes.com. At the time, I wanted to group recipes by their ingredients, but found it difficult due to the way Allrecipes formats each recipe’s ingredient list. So I set myself the challenge of extracting the core of each ingredient description.

The Problem:

Determine each ingredient’s core without supervision

The Constraints:

• No dictionary of ingredients to make the problem easier
• No manually tagging a subset of ingredients

Simplifying Assumptions:

• Each ingredient can be represented by a single word

Unfortunately the simplifying assumption means that pepper, to taste and 1 green bell pepper, diced will both be associated with the same core of pepper, but I found that to make an incredible difference in helping lower the problem’s difficulty.

This is similar to a “most representative subset” problem.

Overview

Two approaches are detailed in this post:

1. Using a linear program to choose the appropriate tokens
2. Using an iterative “learning” approach to choose the appropriate tokens

Note the first method was unsuccessful, while the second proved more successful.

Also note that these are only two of the many methods I attempted. Some were lost in a hard drive failure, and others were just… the worst.

Setup

Data acquisition

I scraped recipes from Allrecipes.com using Selenium, a tool that opens and controls a web browser programatically. A blog post about the scraping is available here.

Data cleaning

First, transforming the output of scraping into a series of ingredients.

# import data
df = pd.read_csv("scraped_data.csv", index_col=0)
df = df[df['ingredients'].notna()]

# unstack each row's ingredients into a single entry in a series of ingredients
df.set_index('recipe_key', inplace=True)

ingredients = df['ingredients'].apply(pd.Series).stack()
ingredients.index = ingredients.reset_index().apply(lambda row:"{}_{}".format(row['recipe_key'], row['level_1']), axis=1).values

Now, what we have looks like:

Ingredient
1 red bell pepper, julienned
1/2 cup heavy cream
1/3 cup firmly packed brown sugar
1/4 cup mango chutney
32 fluid ounces Kentucky bourbon
1/2 cup chopped peanuts
2 tablespoons milk
1/2 teaspoon garlic salt
2 cups thinly sliced red cabbage

The next step is to clean the strings.

My theory was that most ingredients are formatted as follows:

# unit adjective noun, adjective (misc. extra information) - adjectives conjunctions adjectives

Cleaning will include removing digits/anything inside parenthesis, and using lemmatization to combine plurals.

def parse_text(s):
    '''
    Accepts a series of strings, and applies multiple cleaning steps. Returns a series of strings.
    '''
    from nltk.stem import WordNetLemmatizer
    wnl = WordNetLemmatizer()

    def lemmatize(string):
        for word in re.findall(r"[a-z]+", string):
            string = string.replace(word, wnl.lemmatize(word, 'n') if 's' in word[-3:] else word)
        return string
    
    # remove anything inside paranthesis
    s = s.apply(lambda x:re.sub(r"\([^\)]+\)", '', x))
    # remove anything containing a digit
    s = s.apply(lambda x:re.sub(r"\S*\d\S*", '', x))
    # make everything lowercase
    s = s.str.lower()
    # remove plurals where possible
    s = s.apply(lemmatize)
    # remove non-word characters except for , and -
    s = s.apply(lambda x:' '.join(re.findall(r"[-,''\w]+", x)))
    #clean excess whitespace
    s = s.apply(lambda x:re.sub(r"\s+", ' ', x).strip())
    # only keep entries with data after cleaning
    s = s[s!='']
    return s

Looking at a few sample strings:

before	after
30 (2 inch) unbaked tart shells	unbaked tart shell
1 (16 ounce) package uncooked linguine pasta	package uncooked linguine pasta
4 cups all-purpose flour	cup all-purpose flour
2 lemons, juiced	lemon, juiced
1 pound medium shrimp - peeled and deveined	pound medium shrimp - peeled and deveined

All we have to do now is choose the token (word) that represents each full string.

First Approach (miserable failure)

The first attempt relied on an integer program. If you’re unfamiliar with linear (and by extension, integer) programs, check out wikipedia’s entry on the subject here.

Formulation

Generic Formulation (in math):

Formulation (in English):

Choose a subset of tokens (\(x\)) to designate as “core” tokens

With the goal of minimizing the cost of these selected “core” tokens (\(C^T x\))

Subject to:

• every ingredient must contain at least one “core” token (\(Ax \leq b\))
• every ingredient must contain two or fewer “core” tokens (\(Ax \leq b\))
• every entry in \(x\) is binary (associated token is either “core” or is not “core”)

Inputs

First, the constraints: simply using scikit-learn’s CountVectorizer implementation, we can obtain a matrix that looks like:

	token_0	token_1
ingredient_0	0	1
ingredient_1	1	1

In this toy example, token_0 appears in ingredient_1, while token_1 appears in both ingredient_0 and ingredient_1.

Implementation is easy:

def get_A_matrix(s):
    '''Apply CountVectorizer and only retain tokens that are alphabetic.'''
	from sklearn.feature_extraction.text import CountVectorizer
    model = CountVectorizer(binary=True, stop_words=None, ngram_range=(1, 1),
                       tokenizer=lambda x:nltk.word_tokenize(x))
    data = pd.DataFrame(model.fit_transform(s).todense(), index=s.index, columns=model.get_feature_names())
    return data.loc[:, [x.isalpha() for x in data.columns]]

Now, each row of A is a representation of each ingredient description, which we can use to force the linear program to choose at least one token for each ingredient.

More complicated is the penalties. For each token, we need a penalty associated with choosing that particular token as a “core” ingredient.

I decided to penalize 4 things. If a token:

1. appears after certain strings (usually punctuation), or
2. appears as the first token in an ingredient, or
3. appears earlier in an ingredient, or
4. has a certain part of speech,

it should be “more expensive”. Each penalty gets its own weight, usually passed as a dictionary.

The colossal function to find these penalties for each token looks like:

def penalties(processed, pos_dict, split_dict, desc_penalty, first_penalty):
    '''
    Returns penalties for each token in processed, penalizing those that appear after strings in split_dict,
    those that appear first in a string with first_penalty, those that appear earlier in strings with desc_penalty,
    and those with parts of speech in pos_dict.
    '''
    def get_split_penalties(processed, split_string):
        '''Penalizes tokens that appear after split_string.'''
        s = pd.Series()

        for lst in processed[processed.str.contains(split_string)].apply(lambda x:x.split(split_string)).values:
            for index, section in enumerate(lst):
                for token in nltk.word_tokenize(section):
                    s = s.append(pd.Series({token:index/(len(lst)-1)}))
        return s.groupby(s.index).mean().rename(split_string)

    def get_pos_penalties(processed, pos_dict):
        '''Penalizes tokens with {part_of_speech:penalty} given by pos_dict'''
        pos_probs = pd.Series({x:nltk.pos_tag([x])[0][1] for x in set(nltk.word_tokenize(' '.join(processed)))}).apply(lambda x:x[:2])
        pos_probs = pd.get_dummies(pos_probs[[x.isalpha() for x in pos_probs.index]])

        for key, prob in pos_dict.items():
            pos_probs[key] = pos_probs[key]*prob
        return pos_probs.max(axis=1).rename('POS')

    def order_penalties(processed, first_penalty, desc_penalty):
        '''Penalizes tokens that appear earlier in strings'''
        from collections import defaultdict
        indices_dict = defaultdict(list)

        for string in processed:
            words = nltk.word_tokenize(string)
            for ind, word in enumerate(words):
                if ind==0:
                    indices_dict[word].append(first_penalty)
                else:
                    indices_dict[word].append(1-ind/len(words))

        return pd.Series({key:np.mean(val) for key, val in indices_dict.items()}).rename('order')*desc_penalty

    # return sum of penalties
    c_T = pd.concat([get_pos_penalties(processed, pos_dict),
                      order_penalties(processed, first_penalty, desc_penalty),
                      pd.concat([get_split_penalties(processed, key)*value for key, value in split_dict.items()], 
                                             axis=1, sort=True)
                     ], axis=1, join='outer', sort=True).sum(axis=1)

    return c_T[[x.isalpha() for x in c_T.index]]

If your eyes just glazed over, that’s normal. Suffice to say the result of penalties(**args) is a series, where the index is a single token (word), and the value is the penalty assigned to it, given **args. A larger penalty means the word should be less likely to be chosen, while a smaller penalty means the word should be more likely to be chosen.

Creating the IP

Wonderful. All we need now is to build and solve the integer program, using PuLP, a user-friendly linear program implementation for Python. Given \(A\), the representation of each ingredient as vector of tokens, and \(C^T\), the penalties associated with each token, we can solve:

def run_IP(A, c_T):
    '''Solve integer min. program with constraints A, penalties c_T, where Ax>=1
    for every row of A.
    '''
    import pulp
    
    # create problem
    pulp.LpSolverDefault.msg = 1
    problem = pulp.LpProblem('ingredient', pulp.LpMinimize)

    # add variables with associated penalty (sum)
    variables = [pulp.LpVariable(token, 0, 1, pulp.LpBinary) for token in A.columns.values]

    problem += pulp.lpDot(c_T.values, variables)
    
    # add constraint that either one or two tokens per ingredient can be selected
    for index, row in A.iterrows():
        c = pulp.LpAffineExpression([(variables[A.columns.tolist().index(token)], 1) for token in row[row>0].index])
        problem += (1<=c)
        problem += (c<=2)
        
    # solve problem
    status = problem.solve()
    print(pulp.LpStatus[status])
    
    return pd.Series([var.value() for var in variables],
                     index=A.columns.tolist(), name='is_ingredient').astype(int)

Just for a sample of the ingredients, and a few (semi-educated guesses) at penalties:

s = ingredients.sample(n=500, random_state=101)
s_clean = parse_text(s)

# build token matrix
A = get_A_matrix(s_clean)

# build coefficient vector
c_T = penalties(s_clean, 
            pos_dict={'NN':.1, 'VB':10, 'JJ':10},
            split_dict={' - ':3, ', ':2},
            desc_penalty=5,
            first_penalty=500)

# check that all tokens are in both places
assert sum(c_T.index!=A.columns)==0

sols = run_IP(A, c_T)

Results

original	core
1 red bell pepper, julienned	[pepper]
8 ounces shredded Monterey Jack cheese, divided	[cheese]
1/3 cup firmly packed brown sugar	[sugar]
1/4 cup mango chutney	[chutney]
32 fluid ounces Kentucky bourbon	[bourbon]
1/2 cup chopped peanuts	[chopped]
2 tablespoons milk	[milk]
1/2 teaspoon garlic salt	[garlic, salt]
2 cups thinly sliced red cabbage	[cabbage, sliced]

Not exactly great. The main problem is that this method doesn’t choose the best “core” token for each ingredient, instead choosing the best for the entire corpus, and then forcing it on the ingredients. Unfortunately forcing the program to choose each ingredient to have only one token produces an infeasible solution (the linear program can not be solved).

Another problem is that somehow chopped and sliced have made their way into the set of “core” ingredients, which is obviously wrong.

While I could continue to fiddle with **args passed to penalties(**args) until chopped was no longer designated a “core” token, that didn’t sound very appealing, and at the end of the day I still wanted a single, most probable “core” for every ingredient.

Second Approach (moderate success)

Rather than an LP, I designed my own method:

1. assign each token a “score” representing its likelihood of being core, based on similar factors to penalties(**args)
2. for each ingredient, choose the most token with highest “score” to represent the overall ingredient
3. update each token’s “score” based on how frequently each is selected as core
4. repeat 3. until desired spread of “scores” is achieved

Why would this work?

• Because egg (or any other token) will be frequent, sometimes appearing by itself (as in 1 egg), but will also occasionally appear with other tokens (perhaps scrambled, yolks, or fried). This method will gradually promote egg’s score, while gradually decreasing the score of other tokens.
• Moreover, because these other tokens have been penalized, this will promote tokens they appear in association with (learning that rice should be the core of fried rice, because fried is not the core of 2 fried eggs.
• Theoretically, this self-reinforcing cycle will produce better results than simply assigning a penalty once and hoping the IP can decide for us.

Inputs

Scores are calculated in much the same way that penalties(**args) produced penalties. Code is long, and very similar to what was previously shown, and so is omitted to save length.

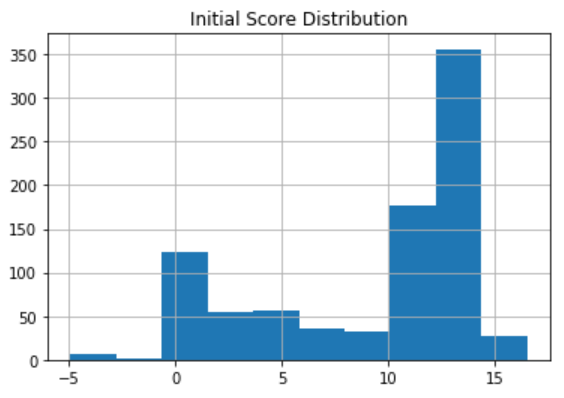
The results of scores(**args) approximately range from -5 up to 15, where a larger score indicates the token is more likely to be “core” than a token with a smaller score.

I forced a few seeds for the first iteration:

• A token will have ranking score of 10 if it ever appears alone (provided it is also a noun)
• A token that ever appears after a hyphen will have ranking score of 0
• Any past-tense verbs that end in ‘ed’ (i.e. crushed, chopped, browned) will have ranking score of 0

This code is also omitted, but simply updates the results of scores(**args).

The distribution of scores looks like:

We now want to force a greater dispersion.

Process

In each iteration, choose a “core” token for each ingredient.

• This “core” token is selected randomly, drawn from a distribution (gained via applying softmax to scores)

We need two functions to accomplish this, one to create the probability distribution (softmax(s)), and one to select the “core” token (pick_max(**args)).

def softmax(s):
    ''' Applies softmax to input series (maps values to (0,1) such that the entries sum to 1.0).
    '''
    e_s = s.apply(lambda x:np.exp(x))
    return e_s / e_s.sum()

def pick_max(row, ranks, seed):
    ''' Selects an entry in row (where row>0), drawn from distribution achieved
    via applying softmax to the ranks. If a seed is included, it will be randomly sampled.
    Otherwise, the entry with maximum probability will be chosen.
    '''
    final = pd.Series().reindex(row.index, fill_value=0).astype(int)
    mask = (row>0)
    if seed:
        index = (row*ranks)[mask].sample(1, random_state=seed, weights=softmax(ranks[mask])).index
    else:
        index = softmax(ranks[mask]).idxmax()
    
    final.loc[index] = 1
    return final

Scores will be updated by using a learning_rate, and “learning” whether each token is “core” based on how often it is selected when it is an option. At each iteration, this process increases the dispersion in scores.

Applying this process iteratively, until a given threshold of dispersion has been achieved in the scores:

learning_rate = 1
threshold = 7.5

while c_T.std()<threshold:
    choices = A.apply(pick_max, ranks=c_T, seed=1, axis=1)
    c_T += norm(choices.sum()/A.sum())*learning_rate

That part, at least, is simple.

The final distribution of scores looks like: 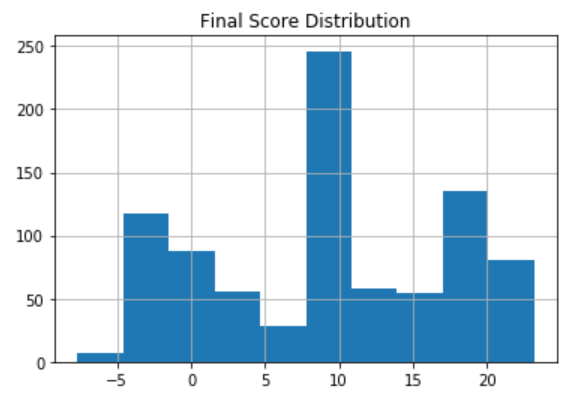Note how the axis have gotten wider as the distribution has spread out.

Results

After the desired threshold of dispersion has been achieved, simply re-choose the “core” tokens, this time selecting that with maximum score, rather than randomly drawing.

# make final choices
choices = A.apply(pick_max, ranks=c_T, seed=None, axis=1)

Looking at choices.idxmax(axis=1):

original	core
1 red bell pepper, julienned	pepper
8 ounces shredded Monterey Jack cheese, divided	cheese
1/3 cup firmly packed brown sugar	sugar
1/4 cup mango chutney	chutney
32 fluid ounces Kentucky bourbon	bourbon
1/2 cup chopped peanuts	peanut
2 tablespoons milk	milk
1/2 teaspoon garlic salt	garlic
2 cups thinly sliced red cabbage	cabbage

Dare I say: eureka?

Conclusions

I mainly attempted this project to prove it could be done, and am quite proud to have achieved what I set out (over a month ago) to do.

A great bonus was building a linear program in Python for the first time (thanks to PuLP).

Areas to expand this project include adding support for “core” tokens that are bigrams or larger - i.e. treating bell pepper as a potential token in its own right. However, I have sunk enough time into this project and achieved sufficient results to walk away happy, though I would be fascinated to see someone else’s attempt to expand what I did, and may re-think my decision to walk away later.

Code

Complete code can be found in my Example Projects git repository, including both the scraper I used to acquire data and the notebook which performs both approaches at extracting “core” text.

See associated requirements.txt for project requirements.