Markov chains for text generation

Concerning Software, using Python on 2020/11/03

text algorithms

Generating believable sentences using Markov chains, based on input text on different topics and in different styles.

• Overview
• Markov chains
  • Text
  • Probabilities
  • Multi-token version
• Implementation
  • Text
    • Processing
    • Cleaning
  • Data structures
    • First word
    • Second word
    • Third and subsequent words
  • Generating sentences
• Results
  • Comments
• Code

Overview

In this post, I’ll use Markov chains to generate text similar to a training corpus.

All code is contained in generate_sentences.py in my software-examples repository, and can be used with any input .txt to generate similar sentences based on a Markov chain of any size.

Markov chains

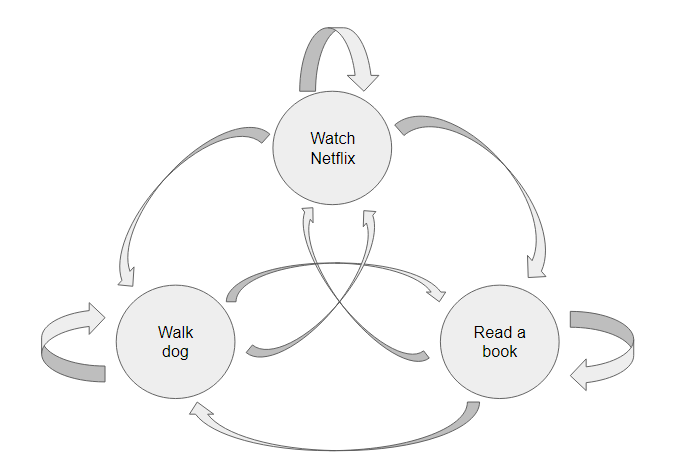
A Markov chain is a mathematical model of a closed system with multiple states. For example, say you’re spending your afternoon at home. Currently, you’re watching Netflix, but at any point, you could go walk your dog, or read a book instead. Visually, we could represent these “states” like this:

Notice that the connecting lines imply we can transfer from any one state to any other - going straight from walking the dog to reading a book, for example.

However, the defining characteristic of a Markov chain, is that it is “memoryless,” which is a fancy way of saying all that matters for what you do next, is what you’re doing now. In this model, you wouldn’t “remember” whether you had walked the dog this afternoon, and so have the same chance of going from watching Netflix to walking the dog after 5 hours of a straight Netflix binge, or if you’ve just sat down on the couch to watch after walking the dog 3 times in a row.

Text

Obviously, Markov chains are a poor mathematical model for a lot of complicated human behaviors. However, they are computationally lightweight, and are surprisingly versatile. In this post, I’ll use them to generate fake (realistic-ish) text.

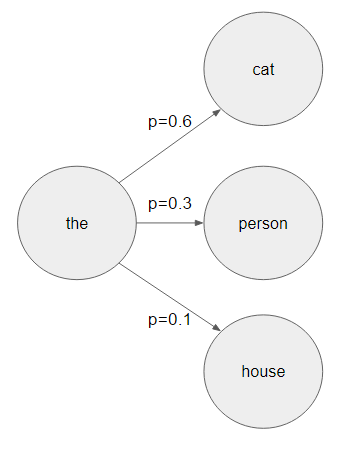
Fundamentally, imagine building a sentence. You start with the first word, say the. Using a Markov chain, we can represent the as our current “state,” and the next word would be any state we could move to next.

In this example, we could be referring to the cat, the person, or the house, with differing probabilities of each (60%, 30%, and 10%, respectively). If we’re randomly generating text, we’d select one of the options from that probability distribution, perhaps giving us the cat, the option with highest probability. Our new state is now cat.

Probabilities

Given that our state is now cat, how do we determine what words (states) are options to follow cat, and how likely they are? The probability examples I just gave were pulled from thin air, but these relationships are learned from a corpus of example text that we’d like our Markov chain to mimic. We could feed in a series of speeches from a politician, a corpus of tweets from a specific account, or an entire book from an author whose prose we’d like to imitate.

Let’s imagine our corpus contained only these three sentences:

The cat ran down some stairs.

A mouse sprinted to get away from the cat.

My cat wanted some milk.

A cat watched patiently.

From these, we can “learn” that the words that come after cat are ran, wanted, watched, and an end of sentence character (. or full-stop). Each are equally likely, so we might draw the full-stop character. Our fake sentence now is the cat., which is quite simple but not incorrect in any way.

With a large enough corpus either on a single topic or from the same author, the Markov chain will calculate accurate enough probabilities for each word-to-word relationship, so that the chain overall will replicate that author (or topic)’s language structure.

Multi-token version

There’s no reason we have to only look at the current word as we’re building a sentence. We can, instead, look at two, or any number, of words when determining the next word to choose.

Let’s do another example on the minimal data, this time using a 2-word Markov chain approach. Say we randomly start with the word A. All we have is a single word, so we have to use a 1-word Markov chain, as before, so our options for words that come after A are cat and mouse, equally likely. Say we randomly choose cat.

Now, our sentence (so far) is A cat. We should consider both words in selecting the next word! Our only option for what comes after A cat is watched. We don’t consider ran, wanted, or the full-stop character, as we did after cat for the 1-word Markov chain example, because neither appear after A cat.

This basic example would end up simply duplicating the last example sentence, A cat watched patiently, but allowing the Markov chain to consider 2 (or more) words when selecting the next dramatically increases the language’s readability.

In generate_sentences.py I’ve included the parameter -m, or --markovsize, indicating how many words to consider when building example sentences.

Implementation

Now that I’ve explained Markov chains and how I’m using them with text, I’ll go over my specific Python implementation that generates the data structures that will power the Markov chains, and that uses these data structures to generate fake text.

Python already has very robust methods for working with text, which I’ll leverage to calculate the word-to-word relationships, primarily leaning on the CountVectorizer class from scikit-learn, and others from nltk and re.

Text

As I mentioned at the start, I’ve written this program to work with any input .txt file, the user simply needs to pass in the path to the file.

For my examples, however, I’ll specifically use two files:

1. The Federalist Papers
2. Submitter descriptions for recipes on Allrecipes.com

Markov chains fit to the first will generate sentences that sound like Hamilton, Madison and Jay supporting the ratification of the US Constitution. They will be more verbose, and use more advanced vocabulary.

Markov chains fit to the second will generate sentences that sound like a recipe description. They will tend to be shorter, and will have a food-based vocabulary.

Processing

Let’s get to the code! Regardless of the input .txt, we need to read it into the computer’s memory, and start working on it.

def make_dictionaries(file_dir, m=2):
    # read in input file
    try:
        with open(file_dir, 'r') as f:
            text = f.read()
    except:
        print("Unable to open input .txt file. Rerun with correct path to input .txt.")
        return

I’ll use a pre-built class from nltk to split the text into individual sentences, storing each sentence as an entry in a pandas Series.

def make_dictionaries(file_dir, m=2):
    ...
    from nltk import sent_tokenize
    import pandas as pd
    
    df = pd.Series(sent_tokenize(text))

Cleaning

I’m going to eventually use the CountVectorizer class from scikit-learn to identify individual words & their associations. Before I can use it though, I need to standardize the text. Here, I’m performing some cleaning functions on the text (lowercase, removing stray punctuation):

def make_dictionaries(file_dir, m=2):
    ...
    # lowercase everything
    df = df.str.lower()
    
    # remove stray apostrophes and parenthesis
    df = df.apply(lambda x:sub(r"((?<=\s)'|'(?!\w))", '', x))
    df = df.apply(lambda x:sub('\"', '', x))
    df = df.apply(lambda x:sub(r"[\(\)\[\]]", '', x))

One thing to note about the CountVectorizer class is it doesn’t handle punctuation very well. As a workaround, I’m going to replace the punctuation I’d like to keep with alternate (unique) text for commas and end-of-sentence characters (exclamation points, question marks, and full-stops).

def sub_endline(x):
    endline = findall(r"\W*$", x)[0]

    if '\!' in endline:
        return sub(r"\W*$", ' eendline', x)
    elif '\?' in endline:
        return sub(r"\W*$", ' qendline', x)
    else:
        return sub(r"\W*$", ' pendline', x)
        
def make_dictionaries(file_dir, m=2):
    ...
    df = df.apply(sub_endline)
    df = df.apply(lambda x:sub(r"(?<=[a-zA-Z]),", ' commaplaceholder ', x))

Data structures

Say the user wants to generate text based on a Markov chain that considers 2 words when choosing the next word. I’m storing this user-supplied parameter -m, or --markovsize, as m, and it defaults to 2.

To actually generate text like this, I’ll need different data structuresfor:

1. The first word of a sentence
2. The second word of a sentence
3. The 3rd and any subsequent words of a sentence

I’ll store these in a list called data_structs, after initializing:

def make_dictionaries(file_dir, m=2):
    ...
    data_structs = [None] * (n+1)

First word

Like what word comes after some given word, I’ll use the observed probability distribution in the training corpus to learn what words typically start sentences.

All I need to store is a list of word options, and how likely each is.

def make_dictionaries(file_dir, m=2):
    ...
    data_structs[0] = df.str.split(n=1).str[0].value_counts()
    data_structs[0] = data_structs[0] / data_structs[0].sum()

This data structure is a pandas Series, with index the word and value the probability. Let’s revisit our minimal example from earlier:

The cat ran down some stairs.

A mouse sprinted to get away from the cat.

My cat wanted some milk.

A cat watched patiently.

In this case, first would look like:

Token	Probability
the	0.25
a	0.5
my	0.25

This indicates our three options for a first word, how likely each is. When we start generating sentences, we’ll randomly draw from this probability distribution.

Second word

Now, we want to build a data structure to power a Markov chain that considers one word when choosing the next. Ignore the loop for now, and just consider when i=1. With prepared data, we can call:

def make_dictionaries(file_dir, m=2):
    ...
    for i in range(1, m+1):
        vect = CountVectorizer(token_pattern=r"(?u)\b[^\s]+\b", analyzer='word',
                                   ngram_range=(i+1,i+1))
        vect.fit(df)

We’ve now “fit” the CountVectorizer to our data, or rather taught it what words are available.

Really important to note - ngram_range=2. When I call vect.fit(df), I’m asking the CountVectorizer to “learn” what word pairs exist (for example, the cat, cat ran, and ran down). When I call vect.transform(df), it will tell me how many of each pair exists in each sentence, but all I care about is how many of each pair exist overall, so I’ll just sum it up and stick the frequencies in a pandas Series, pairs.

def make_dictionaries(file_dir, m=2):
    ...
    for i in range(1, m+1):
        ...
        # get occurrences out of vect
        pairs = pd.Series(np.asarray(vect.transform(df).sum(axis=0)).reshape(-1),
                  index=vect.get_feature_names(), name='freq')
        pairs.index.name = 'tokens'

For our minimal example, the first few items in pairs would look like:

tokens	freq
the cat	2
some stairs	1
some milk	1

All that’s left to do is split the token column into a word, response pair, group by word, and get probabilities for each different response option.

def make_dictionaries(file_dir, m=2):
    ...
    for i in range(1, m+1):
        ...
        # expand to 2 columns (prompt, response)
        pairs = pairs.reset_index()
        pairs = pd.concat([pairs['tokens'].str.rsplit(n=1, expand=True).rename(columns={0:'prompt', 1:'response'}),
                      pairs['freq']], axis=1)
                      
        # undo endline/comma substitutions
        pairs['prompt'] = pairs['prompt'].apply(lambda x:sub(r"\s*commaplaceholder", ',', x))
        pairs['response'] = pairs['response'].apply(lambda x:sub(r"\s*commaplaceholder", ',', x)).replace('pendline', '.').replace('qendline', '?').replace('eendline', '!')

        # store results in a dictionary
        doubles = {}
        for token, group in pairs.groupby('prompt'):
            doubles[token] = {'prob':(group['freq']/group['freq'].sum()).values,
                             'token':group['response'].values}
            
        data_structs[i] = doubles

Notice I’m using a dictionary, doubles, which as it’s key will have a prompt token, and the value will be another dictionary, mapping token to a list of second token options, and prob to the probabilities associated with each combination.

Returning to our minimal example, doubles['cat'], the entry for cat, would correspond to a dictionary mapping token to ["ran", "wanted", "watched", "."], and prob to [0.25, 0.25, 0.25, 0.25].

Note that ths dictionary is being stored in data_structs at i, which is actually the number of words to use when building the Markov chain, as mentioned before. Here, i=1, indicating the Markov chain considers a single word when choosing the next.

Third and subsequent words

The exact same code can be used to accomplish this, we just loop for i=2.

This time through the loop, CountVectorizer will have an ngram_range=(3,3), indicating to count 3-word groups. We’d split the last word off, and use the first 2 as the prompt, and the last as the response. These options & their frequencies would be stored in a new doubles, exactly the same as before.

For our minimal example, doubles['the cat'] maps token=['ran, '.'] and freq=[0.5,0.5], indicating that the options for words after the cat are ran and ., with equal likelihood.

This map would be stored in data_structs[i] (data_structs[2]).

Note that if we wanted a Markov chain to consider even more words when choosing the next, we simply need to increase the user-input parameter m, so that the loop continues for i=3, i=4, etc. Those data structures will be stored and used, the same as the smaller ones.

Generating sentences

With all our data in a friendly format, all we need to do is randomly select a first word from data_structs[0], using that probability distribution, then use that word to find the next, using the options/probabilities in data_structs[1], then the next, using data_structs[2].

We’ll repeatedly continue to draw new words from data_structs[2] until there’s no next token. Generally this should happen when we reach an end-of-sentence character, such as a full-stop, as there are no pairs mapping a full-stop to a next word.

def generate_sentences(data_structs):
    from numpy.random import choice
    from re import sub

    word = choice(data_structs[0].index, p=data_structs[0].values)
    sent = [word]
    
    m = len(data_structs) - 1

    i = 1
    while True:
        try:
            token = ' '.join(sent[-m:]).replace(' ,', ',')
            next_word = choice(data_structs[min(i, m)][token]['token'], p=data_structs[min(i, m)][token]['prob'])

            sent.append(next_word)
            i += 1
        except KeyError:
            # no next token, exit loop
            break

    # join words into complete sentence
    return sub(r"\s(?=[^\w])", '', ' '.join(sent)).capitalize()

Results

Earlier, I mentioned using the Federalist Papers and recipe descriptions as my examples.

Here are 3 sentences built with either 1-word, 2-word, or 3-word Markov chains, all with a random seed of 1:

Recipe descriptions, 1-word:

1. Serve with 1 day and beer, chinese lemon juice, or chicken stock and placed in our coconut, specifically request from thailand.
2. Cook at a delicious soup are great with lemon on hand.
3. Some amazing pizza would not for the best melt well in canned corn and potlucks, but made as many different.

Recipe descriptions, 2-word:

1. Serve with a gingersnap crust.
2. I hate cooking.
3. Serve with basmati rice ahead.

Recipe descriptions, 3-word:

1. Serve with a fresh cream cheese dill spread and tomatoes and lettuce on toasty french bread, if desired.
2. Baked with butter.
3. Thai style chicken dish with sun-dried tomatoes, spinach, cheeses and spices is sealed inside wrappers, then baked hot and fresh.

Federalist Papers, 1-word:

1. If there an efficient government because in one moment that no.
2. It will all the latter it, as to us from the states which at a defense.
3. The latter within the press, that there are supported these qualities, there are liable to defray from both abroad.

Federalist Papers, 2-word:

1. If there are such things as political axioms, the propriety of a previous adoption, as the constitution has supplied a material omission in the articles of confederation.
2. The latter within the limits of their duty but this stern virtue is the growth of few soils and in the one case as to the order of society, and have occasioned an almost universal prostration of morals.
3. Experience, and would essentially embarrass its measures.

Federalist Papers, 3-word:

1. If there are such things as political axioms, the propriety of a previous adoption, as the constitution has supplied a material omission in the articles of confederation.
2. The latter within the limits of their duty but this stern virtue is the growth of few soils and in the one case as to the order of society, and have occasioned an almost universal prostration of morals.
3. Several departments, is not among the vices of their constitution.

Comments

The difference in vocabulary is striking.

All the recipe sentences are obviously about food, though the 2nd 2-word sentence, I hate cooking. is very humorous to me. I imagine it’s due to the prevalence of submitters commenting that they “hate cooking, but…” before alluding to this particular recipe being worthwhile, or easy.

The difference in grammar between the different lengths of Markov chain sentences is also dramatic. The 1-word sentences tend to ramble, especially after commas, and aren’t cohesive as a whole. Conversely, the 2-word sentences are more structurally sound and flow better together, but still ramble from topic to topic. The 3-word sentences are perhaps the best, but still don’t necessarily follow good grammatical structure.

However, while longer Markov chains produce more realistic-sounding text, they also risk being overly constrained to the point of duplicating sentences in the training text.

Code

The full code is available in generate_sentences.py in my software-examples repository.

generate_sentences.py usage:

--filename FILENAME, -f FILENAME
                    Path to raw .txt file. If none is provided, defaults
                    to most recently-created dictionaries.
--simulations SIMULATIONS, -s SIMULATIONS
                    the # of random sentences to build, defaults to 10
--markovsize MARKOVSIZE, -m MARKOVSIZE
                    the # of tokens to consider when building sentences,
                    defaults to 2
--randomseed RANDOMSEED, -r RANDOMSEED
                    the random seed to use when building sentences,
                    defaults to 1