Advent of Code 2020: favorite challenges

Overview
This December, I counted down to Christmas with the Advent of Code, a series of 50 progressively more difficult programming challenges, spread over 25 days. The goal? Complete all the problems successfully, and earn 50 stars. Which I did!
50 virtual stars never felt so good.
Bragging aside, this was an extremely rewarding experience, and I’m proud to have pushed through and finished. Each challenge was new and interesting, and I learned a bunch of new techniques.
My full code for each day’s problems is available in my GitHub repository for AoC 2020. In this post, I’m going to walk through my 3 favorite problems & solutions.
Challenge format
Generally, each day consists of a 2-part programming challenge, usually requiring some text input provided by the challenge website.
For example, on day 1 I was provided a list of numbers, and asked to find the two entries that sum to 2020 for part 1. Part 2 is always similar, and relies on the same input as part 1, but usually requires you to extend your logic or make it somehow more flexible.
Day 10 - sum of paths
On day 10, AoC users were asked to convert voltage using a series of adapters, where each adapter is rated based on the voltage it can output, and can accept voltage 1 to 3 volts lower than its output.
Each user’s unique input consists of a list of adapter ratings (each a round number).
Implementation: part 1
For part 1, the challenge was to use all the adapters to span from 0 volts to the maximum voltage (in this example, 19 volts), and count how frequent each voltage “jump” is - for example, going from an adapter rated 15 to an adapter rated 16 is a 1 volt jump.
Implementation was rather simple. First, read in the input file, and assemble all the adapter voltages into a sorted list (lowest to highest voltage). Additionally, take into account that we are starting at 0 volts and ending at 3 volts above the maximum rated adapter by adding 2 voltages to the list.
with open('day10.txt', 'r') as f:
txt = f.read().strip()
f.close()
voltages = sorted([int(x) for x in txt.split()])
voltages = [0]+voltages+[voltages[-1]+3]
Then, rather simply, iterate through the voltages, finding each “jump”: the difference between adapter[i] and adapter[i-1]. I used a dictionary ranges to store the number of each type of jump.
def count_jumps(voltages):
ranges = {1:0, 2:0, 3:0}
for i in range(1,len(voltages)):
jump = voltages[i]-voltages[i-1]
ranges[jump] += 1
return ranges[1]*ranges[3]
AoC requested the # of 1-volt jumps multiplied by the # of 3-volt jumps as output.
Implementation: part 2
For the second star of day 10, instead of using all the adapters, we needed to count how many ways they can be arranged to still span 0 volts to 3 volts above the maximum adapter.
Now, whenever a problem asks you to “count how many ways…” to do something, the first thought is brute force, in this case trying every combination of adapters and seeing which combination is valid. However, these approaches are never computationally efficient, and moreover, we are given an explicit hit in the instructions not to brute-force:
Luckily, brute force is not required! All we need to know is how many valid paths would take us from voltage 0, through some collection of adapters, and out at 3 greater than the max voltage.
Let’s look at an example for clarity. Suppose we have the following list of adapters (sorted for clarity):
(0) 1 2 3 5 8 10 11 (14)
We’ll start at voltage 0, and end at voltage 14. How many “paths” through the adapters are possible?
I propose the data structure paths, where paths[i] indicates the number of paths to reach the adapter with voltages[i]. In our example, paths[4] would indicate how many ways there are to reach the adapter rated for 5 volts. paths[-1] will be our goal, how many valid paths get us to the ending voltage!
Let’s build paths now. We know that paths[0] = 1, because there’s only 1 way to start: we have 0 volts by default as part of the problem.
How about paths[1]? This is the 1 volt adapter. There’s only 1 way to reach it: from the starting voltage, so paths[1] = 1.
Now, at paths[2], the 2 volt adapter, we have a choice. Remember that each adapter can accept voltage 1 to 3 volts lower than its output, so the 2 volt adapter can accept 1 volt, or 0 volts as input. We could “get here” from the 1 volt adapter, or from the start at 0 volts. Therefore, paths[2] = paths[0] + paths[1] = 1 + 1 = 2.
See the pattern forming? Looking at paths[3], the 3 volt adapter, we know it can accept 0, 1, or 2 volts as input. Generalizing, let’s remember that all our paths need to start at 0 volts. We can get to the 3 volt adapter from the 2 volt adapter (using either of the 2 paths that exist to get there, tracked in paths[2]), the 1 volt adapter (using the 1 path that exists to get there, tracked in paths[1]), or the 0 volt start. So paths[3] = paths[2] + paths[1] + paths[0] + 1 = 2 + 1 + 1 = 4.
Programatically, we want to walk through the adapter voltages, starting at 0. For each adapter voltage, we’ll “look back” at the 3 previous voltages (adapters are unique, so no more than 3 previous adapters could be within 3 volts of the current adapter’s voltage rating). For the adapters within reach (no more than a 3 volt difference), sum the # of paths to each previous adapter to get the # of paths to the current adapter.
def count_paths(voltages):
paths = [1] + [0] * (len(voltages) - 1)
for i, volt in enumerate(voltages):
# at most the 3 previous voltages could connect to current voltage
for j in range(i - 3, i):
# check if voltages[j] is in range of volt
if(volt - voltages[j] <= 3):
# sum up to 3 paths
paths[i] += paths[j]
return paths[-1] # how many different ways to get to last entry (goal)
Given our initial adapter set:
(0) 1 2 3 5 8 10 11 (14)
paths will look like [1, 1, 2, 4, 6, 6, 6, 12, 12]. And there are 12 unique ways to reach voltage 14!
What’s so special?
The fun part to me about coding challenges like this is finding little shortcuts to make the program more efficient. Checking a smaller set, sorting in advance, or sometimes caching results can sometimes have huge performance implications.
I loved day 10 because you had to smartly realize how to walk the possible paths, without performing unnecessary calculations. Brute forcing would’ve required to iterate through every possible permutation, then walk along each adapter configuration, checking if it’s valid. The compute time for a large set of adapters would be immense.
Instead, with this method, we can sort the adapters at the start, and visit each once, simply checking what other adapters are “within reach”.

Fewer calculations, and a simple running sum to take a complicated problem to a simple, elegant one.
Day 13 - least common multiple
On day 13, AoC users were asked to decipher a bus schedule, first finding the soonest bus to depart after a specific time, and next by finding a special time, when all the bus arrivals line up.
As input, each user got 2 lines; the first representing your arrival time at the bus stop, the second representing the frequency that each bus line runs on. For example:
This input indicates you will arrive at the bus stop at 939, and can choose between bus routes that run every 7, 13, 59, 31, and 19 minutes (all starting at time = 0). Buses marked x can be ignored as out of service.
Implementation: part 1
So in part 1, the challenge was simply to determine what bus departs soonest after you arrive at the bus stop. Since each bus line arrives at a constent pace, we can use modular arithmetic to find the smallest difference between each bus line arriving and our arrival at the bus stop.
First off, reading our input data into departure_time (an integer, in our example 939), and IDs, a list with each element representing a bus line frequency.
with open('day13.txt', 'r') as f:
txt = f.read().strip()
f.close()
departure_time, IDs = txt.split()
departure_time = int(departure_time)
IDs = [int(ID) if ID!='x' else ID for ID in IDs.split(',')]
Now for modulo! We know each bus i departs with frequency IDs[i], so rounding up IDs[i] / departure_time gives us the departure # of bus i after we arrive at the bus stop. The time between our arrival and this departure time is the amount of time we would have to wait to catch this bus.
All we have to do is iterate through each bus ID in IDs, calculating the wait time for each bus line, and keeping track of the minimum.
def part_1(IDs, departure_time):
from math import ceil
min_ID = 0
min_wait = IDs[0]
for ID in IDs:
if ID=='x':
continue
wait_time = ceil(departure_time/ID)*ID - departure_time
if wait_time<min_wait:
min_wait = wait_time
min_ID = ID
return min_ID*min_wait
AoC requested the ID of the bus line with minimum wait, multiplied by the wait time as output.
Implementation: part 2
In part 2, the question is when is the earliest time that each bus line departs on the schedule given by input order? In our example where input order is 7,13,x,x,59,x,31,19, we want to find a time t where bus 7 departs at t, bus 13 departs at t+1, any or no bus departs at t+2 and t+3 due to the x, bus 59 departs at t+4, any or no bus departs at t+5, etc.
Clearly, we have a system of equations here:
t % 7 = 0(t+1) % 13 = 0(t+4) % 59 = 0
Due to the modulo operators, it is difficult to resolve these equations. We are again faced with brute-forcing (should we check every time from here to infinity to see if it meets the requirements for t?), and the trick to day 13 is making the search much more efficient by leveraging the least common multiple.
Let’s look at a super small example to get a feel of the math: 2,x,3,11, which indicates we want to find time t when:
t % 2 = 0(t+2) % 3 = 0(t+3) % 11 = 0
Both bus 2 and bus 3 initially depart at time 0. Theoretically, we should check every 1 minute (brute-force), to see if it meets the criteria. However, we know that every 2 minutes, bus 2 will arrive, so there’s no reason to check t = 1, 3, 5..., etc. We’ve halved our search space, but it can be better!
We know the conditions of our “system” (currently, only equation 1) are met every other minute (0, 2, 4, 6, etc). We need to find the first of these intermediate solutions that also fulfill the conditions for equation 2 ((t+2) % 3 = 0). We’ll check 0 and 2, and neither will make equation 2 true, but 4 will.
Now, our system is the first 2 buses, and every 4 minutes they meet our first 2 conditions (equations 1 and 2). We’ve quartered our search space!
We search t = 4, 8, 12..., etc, looking for an (overall) solution that will fulfill equation 3. Finally, we find that t = 52 fulfills all 3 equations.
If we had a 4th equation, we would only have to check every 52nd time slot. The computational savings grow quickly!
Implementation is simple: start by checking every time slot (lcm = 1), and increment lcm as we check buses, decreasing our search space each time.
def part_2(IDs):
# store (divisor, remainder) pairs
B = [(int(IDs[k]), k) for k in range(len(IDs)) if IDs[k] != 'x']
lcm = 1
time = 0
for i in range(len(B)-1):
# update least common multiple for all buses including bus i
lcm *= B[i][0]
# find interval and remainder for next bus
bus_id = B[i+1][0]
idx = B[i+1][1]
# while next bus doesn't arrive at appropriate time, increment time by lcm
# aka proceed to next time increment where every previous bus arrives appropriately
## until we find a time where this bus also arrives appropriately
while (time + idx) % bus_id != 0:
time += lcm
return time
What’s so special?
The code for day 13 isn’t what’s so exciting - it’s the math! It’s been a while since I took number theory and digging up the Chinese Remainder Theorem isn’t generally part of my day job, but this was an incredibly fun problem. Luckily, my input bus IDs were all prime, which enables this mathematical shortcut.
Seeing the search space decrease so rapidly is incredibly satisfying. 
Day 23 - linked list
On day 23, AoC users were asked to simulate many rounds of a puzzle game where labelled cups are arranged in a circle, and re-arranged each turn following a set of rules.
The puzzle input is a set of numbers, where each number represents a single cup. The game starts with the first labeled cup as the current cup, and each round proceeds as follows:
- Remove the 3 cups immediately clockwise of the
current cup. - Find the
destination cup, the cup labeledcurrent cup - 1. (If this cup was removed, continue tocurrent cup - 2and so on, wrapping around to the highest cup number if necessary) - Move the 3 removed cups to immediately clockwise of the
destination cup. - Find the cup that is now immediately clockwise of the
current cup. This is thecurrent cupfor the next round.
For example, the starting layout 389125467 indicates 10 cups, starting with the cup labeled 3, arranged clockwise in a circle.
The current cup is 3, and we remove the 3 cups immediately clockwise of it: 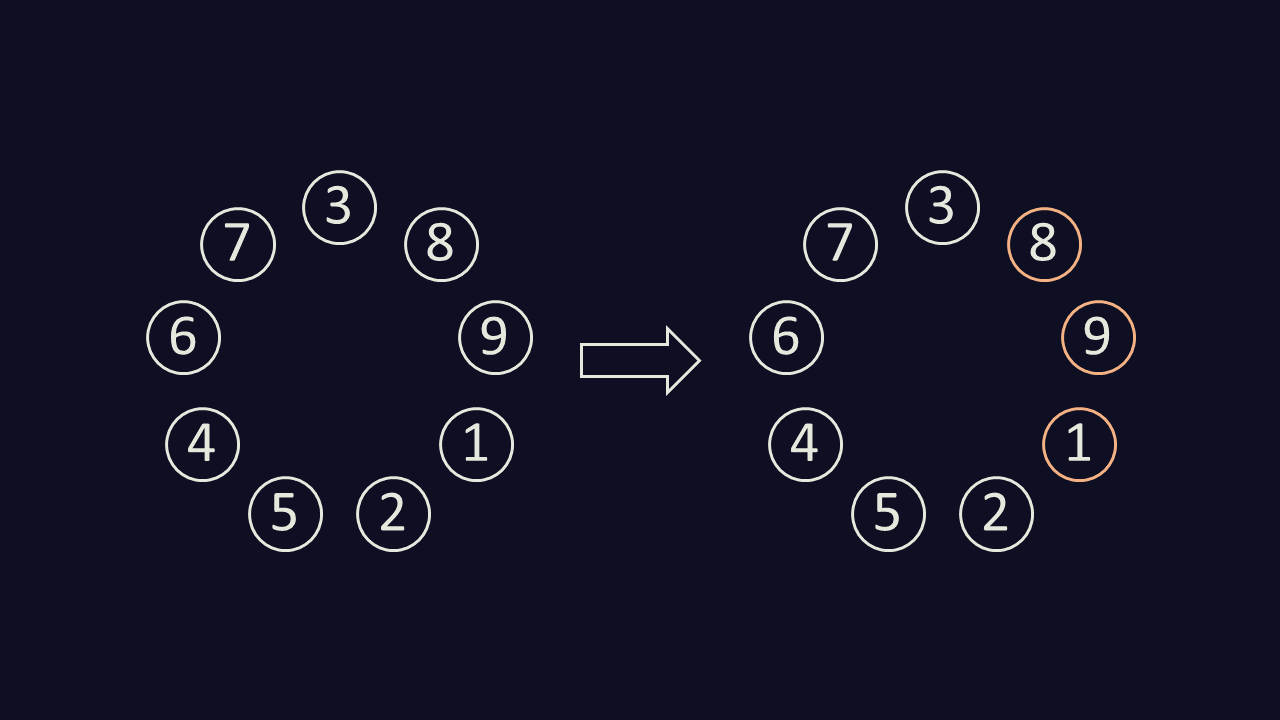
We find the destination cup by looking for current cup - 1, which is cup 2. We then complete the circle by inserting the removed cups immediately clockwise of the destination cup: 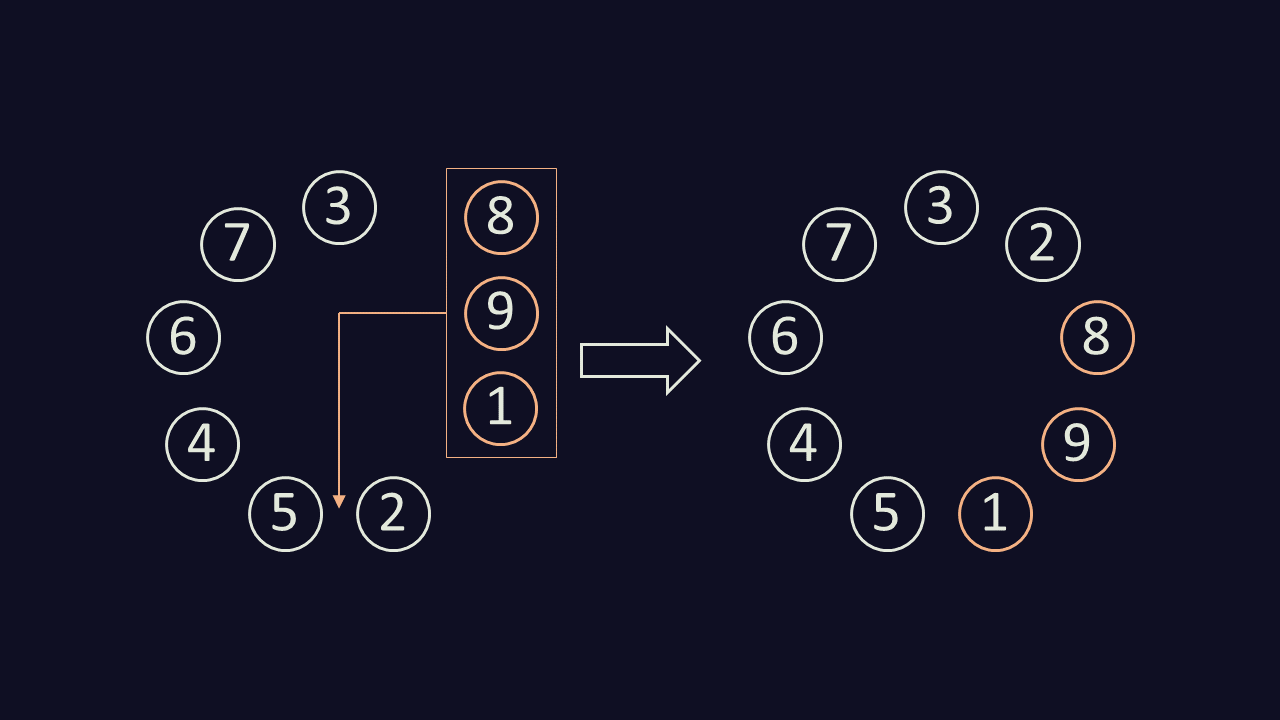
Lastly, find the cup immediately clockwise of the current cup, and use it as the current cup for the next round.
Implementation
Part 1 and part 2 are the same problem - both require simulating a number of rounds of gameplay. Part 1 is very small (100 moves), and simply requires you to correctly implement the game logic. However, part 2 requires you simulate ten million (10,000,000) moves, essentially stress-testing your implementation. The key to this day’s problem is an efficient implementation of re-ordering the cups each round.
To maintain order as the cups are rearranged in a circle, I decided to implement a linked list via a python dictionary. order will map a cup label to the cup immediately clockwise.
def play(starting_order, n):
with open('day23.txt', 'r') as f:
txt = f.read().strip()
f.close()
starting_order = [int(x) for x in txt]
order = {}
for i in range(-1,len(starting_order)-1):
order[starting_order[i]] = starting_order[i+1]
In our example from earlier, 389125467, order[3] = 8, order[8] = 9, etc. Importantly, we must also “close the circle”, tying order[7] = 3, which I accomplish by starting the loop at i = -1.
Now, remember that each round, we remove then relocate 3 cups, maintaining their order?
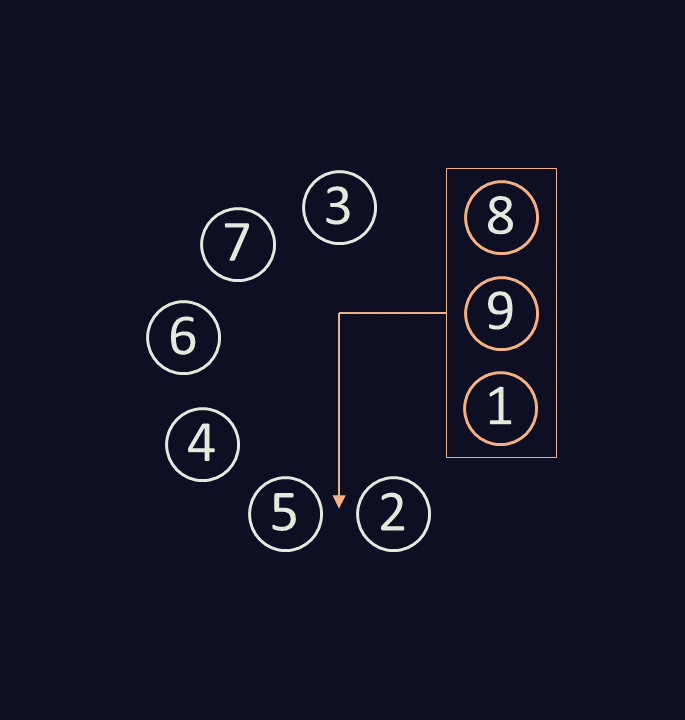
With the linked list implementation, we only need to update 3 things:
- Close the “gap” where the 3 cups were removed (connecting
cups[3] = 2) - Insert the last of the removed cups just after the destination cup (connecting
cups[1] = 5) - Insert the first of the removed cups just before the destination cup (connecting
cups[2] = 8)
To do this, I’ll first select the 3 cups to remove, and take note of the cup after the new “gap” (cup 2).
def play(starting_order, n):
...
start = starting_order[0]
for round in range(n):
# take out 3 cups
removed_1 = order[start]
removed_2 = order[removed_1]
removed_3 = order[removed_2]
after_removed = order[removed_3]
taken_out = [removed_1, removed_2, removed_3]
Next, we have to find the destination cup by searching for current cup - 1. Luckily, we know that if that cup has not been removed, it is available as a destination. Otherwise, we need to continue the search, potentially wrapping around to the maximum cup value.
def play(starting_order, n):
max_cup = max(starting_order)
...
for round in range(n):
...
# find destination cup
search_cup = start-1
while True:
if search_cup<=0:
search_cup = max_cup
if search_cup not in taken_out:
destination_cup = search_cup
break
search_cup -= 1
Now that we know where the removed cups are going, all we need to finish the round is to update our 3 entries in order, and find our new current cup, stored as start.
def play(starting_order, n):
...
for round in range(n):
...
# connect "hole" where taken out cups are being removed
order[start] = after_removed
# connect last taken out cup to the next after destination cup
order[removed_3] = order[destination_cup]
# connect destination cup to 1st taken out
order[destination_cup] = removed_1
start = after_removed
return order
As output, AoC requested the new cup order at the end of all rounds.
What’s so special?
In python, other ordered data structures (such as a list) would be much more computationally costly to update (or re-build) each round with the new cup order. Since the majority of the inter-cup relationships don’t change, there is no reason to dramatically overhaul the data structure each time. With 3 simple updates to a dictionary, we can represent the structural changes as we remove and insert cups each round.

Despite the initial complexity of the problem, the code to implement (once I figured out the shortcut) was short and sweet. This was my favorite challenge implementation of the whole month of programming problems, thanks to how simple the logic becomes by maintaining the circular structure.
Code
The full code is available in my GitHub repository for AoC 2020.
Generally, dayx.py accepts dayx.txt as input, and outputs the 2 numbers that AoC requests as puzzle solutions (typically 1 for part 1, and another for part 2).

